4.4 Base y dimensión de un espacio vectorial, cambio de base.

-
Se ha visto en R2 conviene escribir vectores como una combinación lineal de los




 En R3 se escribieron los vectores en términos  de






Ahora se generalizara esta idea.
BASEUn conjunto finito de vectores  es una base para un
espacio vectorial V si
Todo conjunto de n vectores linealmente independiente en Rn es una base en Rn.
En Rn se define   
Puesto que los vectores e, son las columnas d una matriz identidad (que tiene
determinante 1),  por lo tanto, constituye una base en Rn. Esta base especial se denomina base canonica en Rn. Ahora se encontraran bases para otros espacios. 

EJEMPLO: base canonica para M22 

Se vio que  generan



entonces es evidentemente que  Así, estas cuatro 
matrices son linealmente independientes y forman una base para M22, lo que se
denomina base cononica para M22 

TEOREMA: si es una base para V y si vÎV, entonces existe un 
conjunto único de escalares tales  que



Existe cuando menos un conjunto de dichos escalares porque  
genera a V. suponga entonces que v se puede escribir e dos maneras como una
combinación lineal de los vectores de la base. 

Es decir, suponga que dos bases para V. debe 
demostrarse que m=n. esto se prueba mostrando que si m>n, entonces S es un
conjunto literalmente independiente, lo que contradice la hipótesis de que S es una
bse. Esto demostrara que m≤n. la misma prueba demostrara que ≤m y esto
prueba el teorema. Así, basta demostrar que si m>n, entonces S es
independiente. Como S constituye una base, todo u se puede expresar como una
combinación lineal de las v. se tiene 





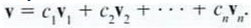
Comentarios

Publicar un comentario

Entradas populares de este blog

3.4 Métodos de solución de un sistema de ecuaciones lineales: Gauss, Gauss-Jordan, inversa de una matriz y regla de Cramer.

-
Imagen
MÉTODO DE RESOLUCIÓN DE GAUSS-JORDAN Es el método de resolución de sistemas de ecuaciones lineales, que consiste en llegar a un sistema "escalonado" transformando la matriz ampliada en una matriz escalonada por filas. El método de Gauss es una generalización del método de reducción, que utilizamos para eliminar una incógnita en los sistemas de dos ecuaciones con dos incógnitas. Consiste en la aplicación sucesiva del método de reducción, utilizando los criterios de equivalencia de sistemas, para transformar la matriz ampliada con los términos independientes ( A* ) en una matriz triangular, de modo que cada fila (ecuación) tenga una incógnita menos que la inmediatamente anterior. Se obtiene así un sistema, que llamaremos escalonado, tal que la última ecuación tiene una única incógnita, la penúltima dos incógnitas, la antepenúltima tres incógnitas, ..., y la primera todas las incógnitas. El siguiente esquema muestra cómo podemos resolver un sistema de ecuaciones l...
Leer más

5.4 Aplicación de las transformaciones lineales: reflexión, expansión, contracción y rotación

-
Rm.◊Graficar un conjunto de puntos en otro es lo que se conoce como transformación lineal de un conjunto de puntos. Existen ciertas propiedades básicas de las transformaciones lineales, las cuales si son tomadas en cuenta y aplicadas al momento de resolver un problema, pueden reducirlo un problema simple. La notación general utilizada para una transformación lineal es T: Rn  Transformaciones lineales  Las transformaciones lineales forman un “hilo” que se entreteje en la tela de este texto. Su utilización mejora el sentido geométrico de lo escrito. Por ejemplo, en el capítulo 1, las transformaciones lineales proporcionan una visión dinámica y gráfica de la multiplicación matriz-vector.  1. Reflexión: Cuando un conjunto de puntos dados es graficado desde el espacio euclidiano de entrada a otro de manera tal que este es isométrico al espacio euclidiano de entrada, llamamos a la operación realizada la reflexión del conjunto de puntos dado. Esto pued...
Leer más